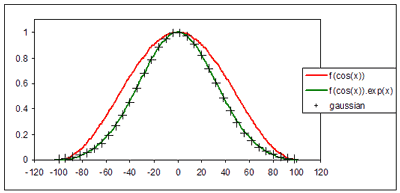
Peak roughening

One method of making heightfields is to 'deposit' onto a flat heightfield a large number of geometric shapes like cones, pyramids or hemispheres. Prime examples of terrain made by this technique are shown on www.robot-frog.com (Bob Nystrom), using hemispheric peaks, and www.lighthouse3d.com (António Ramires Fernandes), using sinusoidal peaks.

The task of making the approximate land-shape in L3DT is handled by the design/inflate routine, but peak overlays are added to make rolling hills on a scale smaller than a design-map pixel (64×64 heightfield pixels). The shape of the peaks used approximates a Gaussian curve (as of L3DT 2.2), but with a finite skirt, and is shown in the figure below (green curve labelled 'f(cos(x))*exp(x)').

Profile of several peak overlay functions

The mathematical form of the curve is:

y = e^r-1 × (1 - cos(πr)) ⁄ 2

where the radius r = 0..1.

The red curve is the cosine-based peak shape used previously in L3DT, with the mathematical form:

y = (1 - cos(πr)) ⁄ 2

These peaks made the map look a bit too lumpy.

The extra calculation time for making such mathematically complex these peaks is negligible because L3DT only generates 6 or so peak overlays (with different radii) and applies them many many times with random vertical scaling. The peaks are applied early in the inflation/overlay algorithm when the heightfield is at 1/16^th final map resolution (or 1/256^th final map area). The upshot is that the routine is pretty quick.

All these peaks are radially symmetric. I have tinkered with asymmetric peaks, but I found the computation penalty in generating and rotating such overlays to be quite unreasonable.